Introduction to Regularizing 3D Data – Part 2 of 2

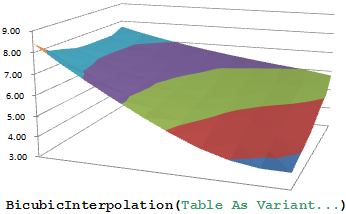
An Entire 3D Surface from a Few Measured Points

• An investment banker needs to create an entire volatility surface from a handful of derivatives trades that took place today.
• A chemist needs to know the temperature near the center of a reaction chamber based on only a few temperature measurements scattered around its perimeter.
• An engineer needs to model something with a smooth function of two variables, but he doesn’t know the function and all he has are a few dozen noisy measurement points.

How do they do it? By regularizing their 3D data of course!

The first part of this article showed how we use bilinear interpolation to relate arbitrary input points to locations on an output grid. Now we will look at the fidelity equations, set up second-derivative equations for the 3D data, and find the least-squares solution. The result is a regularized surface in 3D.

For those who like to see the details, the example spreadsheet is available for download.

Introduction to Regularizing 3D Data – Part 1 of 2

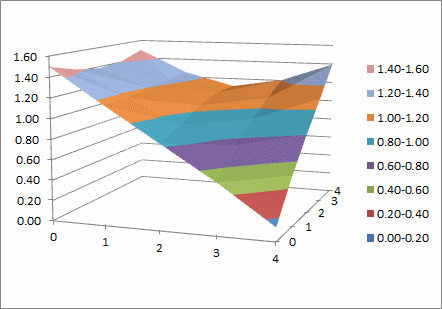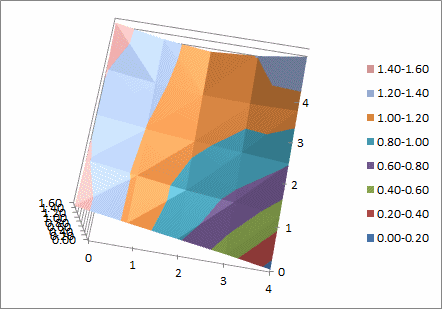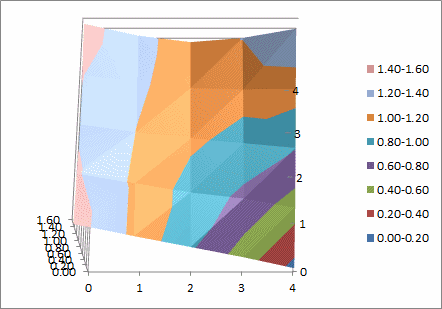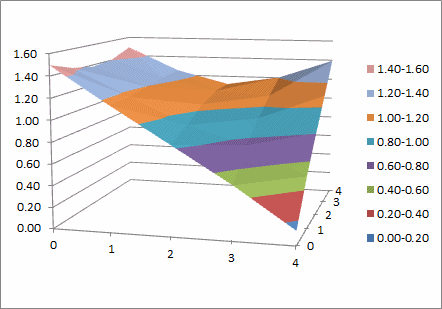How to Regularize 3D Data

This article shows how to regularize data (3D Data) in an Excel spreadsheet using basic spreadsheet functions. This is remarkably similar to the 2D case, except for a few extra steps to handle the 3D data.

This introduction shows how to set up the 2D interpolation and explains the difference between triangle interpolation and bilinear interpolation. It also shows how to set up the second derivatives for 3D data. The Excel spreadsheet is available for download.

Bicubic Interpolation – VBA Function Compatible with Both Arrays Ranges

Bicubic Interpolation – One VBA Function Compatible with Both Arrays and Ranges

People write VBA functions to use in their spreadsheets. People write VBA functions to use in their VBA scripts. How about a single VBA function that works in both script and spreadsheet?

Sometimes your tabular dataset is in a worksheet. Other times it is already in an array and you don’t have any need to copy it to a worksheet. Can you just use the bicubic interpolation function on both? This article shows how to bring versatility to an Excel VBA function for both spreadsheets and VBA scripts using bicubic interpolation as an example.