Cubic and Bicubic Interpolation Excel Functions v3
We have expanded our custom Excel interpolation functions to interpolate both 2D and 3D datasets, i.e. to interpolate over a curve or over a surface.
Cubic and Bicubic Interpolation Excel Examples with Source Code
Cubic Interpolation in Excel
CubicInterpolation() is a spreadsheet formula that interpolates over 2D data. The first argument is a list of x points and the second argument is the list of corresponding y points. These x and y values can be ranges on the worksheet or arrays (if you use the function directly in VBA). They can be in rows or in columns. One can be in a row and the other in a column; this function is very forgiving about how the input is formatted. The example below shows that the interpolation function ignores blank cells at the end of the dataset as in Rows 12-14).
The blue points are the original source data, which are irregularly spaced (note the gaps near x=2.4 and x=2.8) and far apart. The dotted lines represent piecewise linear interpolation. The red dots are points we get from CubicInterpolation() at various locations. These tend to mimic the curvature of the function that would be lost with any kind of linear interpolation. This is one of the benefits of using cubic interpolation.
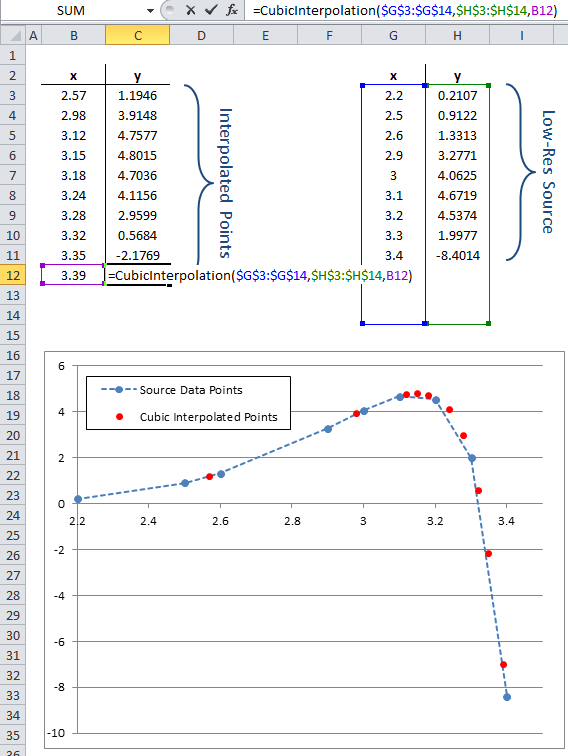
The technique it’s using is piecewise Lagrange interpolation. When you try to interpolate at x, the script looks for the two points in your source data on either side of x. From those four points it constructs a cubic equation by Lagrange interpolation. In other words, the fitting is piecewise cubic. The benefit of piecewise curve fitting is that you can work with highly complicated datasets that do not need to look anything like a cubic function because each fit is local and uses the best datapoints. This helps avoid Runge’s phenomenon (wild oscillations from overfitting).
Bicubic Interpolation in Excel
BicubicInterpolation() interpolates over 3D tabular data, and this older post gives details about how to use it. In summary, the first function argument is the entire table of axes and data like in the example below. The second and third arguments give the location within the table where you want to interpolate. This too is very forgiving with regard to its arguments and where/how it is used. It works as a spreadsheet function or directly in VBA.


The algorithm is similar to the 2D case, except that instead of interpolating over four nearby points, it interpolates locally over 16 points. The second argument is the “top point,” meaning the location along the horizontal axis at the top of the table. The third argument is the “left point,” similarly referring to the axis at the left side of the table. In summary, the syntax follows the pattern: table, x, y. The intent is to be intuitive insofar as the horizontal axis coming before the vertical axis.
With these functions you can do 2D and 3D interpolation in Excel as if you’re using a built-in spreadsheet function.
super duper stuff. I couldnt see any post after April 2014. I hope all is well and the great work continues.
Thanks, Nepa. We will have more posts in the future. You are welcome to put in a request if there is something you would like to see. There will be an update to the Matlab data regularizing function that works in N dimensions.
On Saturday, October 15, 2016, Math for Mere Mortals wrote:
>
This function is great! Is there a way to get the polynomial form coefficients for the interpolated results?
This function is exactly what we needed. Without it, doing linear interpolation, the amount of source data required would have been more than 100X larger. Thanks.
That’s great that it works for you! Let us know if there’s anything else that would be useful.
On Wed, Jul 12, 2017 at 12:46 PM, Math for Mere Mortals wrote:
>
The function is great and just what I needed. When I checked it for output it’s giving error for some values. Hope you can solve my problem. It would be great if we could discuss this in more detail. Thanks
Can you give some information about the errors? It may be possible to fix them quickly.
On Sat, Jul 14, 2018 at 2:22 PM Math for Mere Mortals wrote:
>
Can I use the subprogram “CubicBicubicInterpolation_v3” or other subprograms presented on this website commercially at work?